扩散模型DDPM

介绍

扩散模型的基石：DDPM(Denoising Diffusion Probalistic Models)[2020]

DDPM的本质作用，就是学习训练数据的分布，产出尽可能符合训练数据分布的真实图片。

训练流程

总体来说，DDPM的训练过程分为2步

• Diffusion Process (Forward Process)
• Denoise Process (Reverse Process)

而 DDPM 的目的是要去学习训练数据的分布，然后产出和训练数据分布相似的图片。

思路

拿一张干净的图，每一步(timestep)都往上加一点噪音，然后在每一步里，都让模型去找到加噪前图片的样子，也就是去噪。

训练完毕后，我们再拿出一张纯噪声图，让它帮我们还原出原始图片的分布。

• Diffusion Process:一步步加噪的过程
• Denoise Process:一步步去噪的过程

Diffusion Process

Diffusion Process的命名受到热力学中分子扩散的启发：分子从高浓度区域扩散至低浓度区域，直至整个系统处于平衡。加噪过程也是同理，每次往图片上增加一些噪声，直至图片变为一个纯噪声为止。

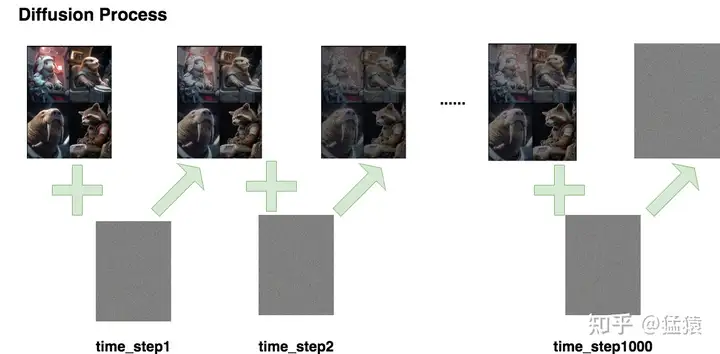
我们对图片进行了1000步加噪，且每一步添加的都是高斯噪声，直到图片变成一个纯高斯分布的噪声。

数字符号标记

• $T$:总步数
• $x_0,x_1,…,x_T$:每步产生的图片。其中$x_0$为原始图片,$x_T$为纯高斯噪声
• $\epsilon \sim N\left( 0,I \right)$:为每一步添加的高斯噪声
• $q\left( xt|x{t-1} \right) $:$xt$在条件$x=x{t-1}$下的概率分布。

根据以上流程，我们有：$xt=x{t-1}+\epsilon=x_0+\epsilon_0+\epsilon_1+…+\epsilon$

但是，为了得到x_t，需要sample好多次噪声

重参数

为了解决这种不方便的情况，我们加入权重。

随着步数的增加，图片的原始信息越少，噪声越多。

于是乎，加入一系列常数$\bar{\alpha}_1,\bar{\alpha}_2,…,\bar{\alpha}_T$，随着T的增加越来越少

此时可以设置为

$$x_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon$$

这时，我们只需sample一次噪声，就可以从x_0得到x_t

那么使得$q\left( xt|x{t-1} \right) $转换成$q\left( xt|x{0} \right) $的过程，就成为重参数

Denoise Process

Denoise Process的过程与Diffusion Process刚好相反：给定xt，让模型能把它还原到x{t-1}。

用$q\left( xt|x{t-1} \right) $来表示加噪过程，则用$p\left( x{t-1}|x{t} \right) $来表示去噪过程

由于加噪过程是按照设定好的超参数进行前向加噪，不存在训练的过程。

但去噪过程是真正训练并使用模型的过程。于是我们再加入一个模型参数

即：$p\theta\left( x{t-1}|x_{t} \right) $

如图，从第T个timestep开始，模型的输入为x_t和当前的t，模型中还包含一个噪声预测器（UNet），它会根据当前的输入预测出噪声，然后，将当前图片减去预测出来的噪声，就得到去噪后的图片。且重复这个过程，直到还原原始图片x_0。

Training

在重参数的表达下，第t个时刻的输入图片可以表示为：

$$x_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon$$

而第t个时刻sample出的噪声$\epsilon \sim N\left( 0,I \right)$，为我们的噪声真值。

预测出来的噪声为：

$$\epsilon _{\theta}\left( \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon ,t \right)$$

则loss为：

$$\epsilon -\epsilon _{\theta}\left( \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon ,t \right)$$

我们要做的是将Loss最小化

由于不管对任何输入数据，不管对它的任何一步，模型在每一步做的都是去预测一个来自高斯分布的噪声。因此，整个训练过程可以设置为：

• 从训练数据中，sample出条x_0
• 随机sample出一个timestep
• 随机sample出一个噪声
• 计算Loss
• 计算梯度，更新模型，重复上述操作，直至收敛

Sampling

将DDPM训练好后，我们该去使用它，并评估它

我们从最后一个时刻（T）开始，传入一个纯噪声（或者是一张加了噪声的图片），逐步去噪。

根据$xt=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon$ 可以推出 x_t与 x{t-1}的关系(具体推导后面解释)

通过上述方式产生的 x_0 ，我们可以计算它和真实图片分布之间的相似度

插值方法

先对两张任意的真实图片做Diffusion过程，然后分别给它们的diffusion结果附不同的权重，将两者diffusion结果加权相加后，再做Denoise流程，就可以得到一张很有意思的”混合人脸”。

这个方法很关键，有启发性，可以试试替代SBI

Unet

我们将它分为2部分

• Encoder
• Decoder

在Encoder部分中，UNet模型会逐步压缩图片的大小；在Decoder部分中，则会逐步还原图片的大小。

时在Encoder和Deocder间，还会使用“残差连接”，确保Decoder部分在推理和还原图片信息时，不会丢失掉之前步骤的信息。整体过程示意图如下，因为压缩再放大的过程形似”U”字，因此被称为UNet.

DownBlock和UpBlock

TimeEmbedding层采用和Transformer一致的三角函数位置编码，将常数转变为向量。Attention层则是沿着channel维度将图片拆分为token，做完attention后再重新组装成图片

需要关注的是，虚线部分即为“残差连接”（Residual Connection），而残差连接之上引入的虚线框Conv的意思是，如果in_c = out_c，则对in_c做一次卷积，使得其通道数等于out_c后，再相加；否则将直接相加

DownSample和UpSample

这个模块很简单，就是压缩(Conv)和放大(ConvT)图片的过程。